Fish Math

The way E thinks about math is fascinating. He has long been interested in equations. I took the photo below last September after he had asked me to come look at some math he did on our easel. He was really proud and thought his work was hilariously clever.

He had started at the bottom of the easel with the numerical equations so that's what I saw first. As I took it in, I first noticed, woah, he's super proud of this; he's smiling, his eyes are alight, and he's excited to share with me. Next, I read through the number sentences and realized he had actually done the math correctly. Last, I took a mental note that he was still writing his numbers with some reversals, still working on using consistent top down, left to right progression, and still printing numbers in his own unique way based on digital fonts. But, because I am familiar with his quirks, none of these "mistakes" get in the way of me understanding or appreciating what he was doing, and I didn't comment on any errors because that would have triggered his threat response. I know that he will self-correct these things on his own time, and I know better than to dampen his creative process with corrections.

So, this is how his thinking progressed:

7+7=14 2+4=6

48+84=130 518+401=919

He had started with single digit addition at the bottom right of the board, then moved towards more complex double and triple digit equations. Interestingly, I noticed he wrote all his number sentences horizontally, even the more complex ones; he has never wanted to learn the vertical addition method of stacking the digits in place value columns (and then carrying the 1, etc.), because he does it all in his head. I have modeled that method for him when figuring out math problems of my own, but he's disinterested because his way works for him.

After showing off his number sentences to me, he told me to go away because he had some more good ideas to add.

He was inspired to write equations with words next:

"Egg + bread = egg sandwich"

"Patty + bun = burger"

"Ice + heat = water"

"Air + air = air"

Or my personal favourite: "Mommy+ very deadly monster= die hahaha"

He called me back to show me and we giggled.

The equation about me and the monster then inspired him to think about Minecraft, and at the top of the easel he began making equations about the game:

"Pond + mob = run" (Pond is his nickname for our nanny)

He soon added drawings and speech bubbles into the mix, to:

"Nether + Pond = die"

Piglin: "She did attack us."

"Mommy + creeper = die"

Creeper: "It wasn't me."

You can see how interconnected math, literacy, art, social interactions, and deep interests are for E. It doesn't make sense for him to have a "math lesson," because math does not stand alone; his learning is a complex and beautiful interdisciplinary experience led by his life and his imagination.

As I saw his equations unfold on the easel and he worked away on his Minecraft sentences, I remembered a wonderful book from my teaching days called This Plus That: Life's Little Equations by Amy Krouse Rosenthal. I remembered being introduced to it in a professional development workshop by Adrienne Gear. We don't own a copy, so I did a quick search and found a read aloud on YouTube. I played it for E when he was finished his work on the easel, telling him I had made a connection between the book and his equations. He was only mildly interested, which made me mildly disappointed. It is such a cute book that connected perfectly to his work! At least to me. I think E preferred to focus on his own ideas, and would have rather not been told that other people before him had also made up clever equations. B and I watched the whole read aloud, and E listened. As the video progressed, however, I noticed he was getting dysregulated by the idea of the book being so similar to his own work, so after the video was over, we moved on and I didn't bring it up again.

It was one of those moments when a connection I had made seemed so perfect as a way to extend E's learning, but that connection, while powerful for me, was not at all what E wanted to hear. This disconnect happens often. All I can do is offer expansions to his world, some he latches on to, and some he does not. It's hard not to take it personally when he doesn't like my ideas, but I'm working on it.

After showing him the video, I didn't hear too much more about equations for a little while until a few weeks ago we had this exchange:

E: "What's 2+2?"

Me: "4."

E: "Wrong!! 2+2=fish!"

Me: "Oh."

E: "What's 4+4?"

Me: "Um... It's not 8...."

E: "No! 4+4= 2 fish! How many is 16?"

Me: "Ummm...16=...4 fish?"

E: "Yes! You passed my test!"

I thought back to his interest in equations from the fall, but didn't tell him I had made a connection to his previous learning. I now knew from my experience that it is better to just let his thinking unfold in the moment so he doesn't feel any loss of autonomy and become activated at the thought that I am trying to "teach" him something.

Similar fish math conversations would pop up every few days, sometimes at the dinner table, sometimes in the car, sometimes while he was just hanging out while I was busy in the kitchen or doing something around the house.

E: "What is 6 fish?"

Me: "Oh.. umm... 2+2=fish, right? So, 6 fish would be... 24?"

E: "Correct!"

Eventually, I caught on that if he brought up any math question he was basically always talking about fish and just started answering every question posed to me with the understanding that fish=4. Each time he brought it up, the riddles would get more and more complex.

E: "What is 32?"

Me: "8 fish?"

E: "Yes! 64?"

Me: "12 fish!"

E: "Yes!"

His fish math is fascinating because I can really see his PDA brain at work. Because I am his parent and someone who generally knows more math than an 8-year-old, his sense of balance and autonomy would feel threatened because my increased knowledge puts me above him, which triggers his threat response. So, instead, to compensate, he has found a playful, creative way to discuss math with me in that puts him completely in the lead and allows him to feel safe. Thus, fish math is born!

The other day as I was grilling chicken for dinner and E was with me in the backyard, pacing in circles as he ate a fudge popsicle, he called over, "Mommy! I'm going to give you some fish math! What is 100+2 in fish language?"

Me (I'm thinking... ok, if 2+2=fish, then fish=4, so100/4=25 with then two left over... so...): "100+2 is 25 fish, remainder 2." (It's also fascinating to me that I haven't used this math terminology of remainders for probably 20 years, and yet, it still popped right out into the proper use!)

E: "Does remainder mean left over?"

Me: "It does."

E: "You got it!"

He has essentially made up his own math language with a combo of algebra (fish, or x, = 4), multiplication, and long division. This equation is what he would have had to have figured out in his head before giving me his quiz:

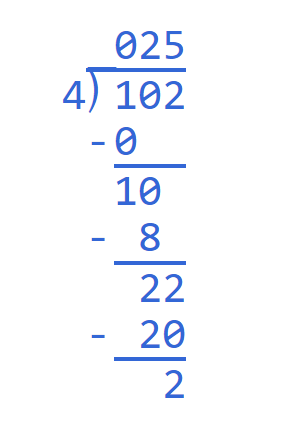
Except he's never heard the term long division, nor been taught the steps that we all likely had drilled into our psyches in elementary school.

His mental math skills have always been exceptional, but he can't always explain how he knows something, he just knows it. He wouldn't be able to write out his process, or "show his work," for a question like this, just like he wouldn't have known how to write out his addition sentences vertically.

Thus, an accommodation I make for him is to make almost all of our math learning discussion-based. Sometimes I tell him I need a pen and paper (because I genuinely do to figure out some of the questions he asks me!) and so I will sit beside him and model long division or multiplication or BEDMAS, or whatever it is, but he is usually disinterested and says something like, "I don't do it like that." And he moves on.

I worry that there will be gaps in his knowledge, or that more complex math concepts will be too difficult later on because he hasn't practiced the steps leading up to his answers. However, I have to surrender to letting him do it his way, not only because he is resolute in his decision to do it that way regardless of what I think, but also because me making suggestions would trigger his threat response and he might become unsafe.

Reminding myself to trust my child, to trust his instincts and his imagination and intellect, is a daily practice, even after 3 years of unschooling. His learning does not follow a traditional route, but he is constantly building on his knowledge in ways that make sense to him.

The day after we chatted about 100+2 in fish language, he told me there are other animals in fish math world.

1+1= kitty

2+2 = fish

4+4 = cow

So together we chatted about how many kitties would be in 100, and how many cows. And then he started solving for fish and kitty and cow for bigger and bigger numbers, 200, 400, 1000, 12,000. And I'm sure more discussions will be had in the coming days, though what they might entail I could not guess!

I told my husband about fish math and, interestingly, while E doesn't like me asking him fish math questions directly because his autonomy feels threatened, he doesn't mind when my husband asks him. So he is now answering equations made up by someone else as well as asking us. We still need to follow his lead about when he is in the mood for fish math, and not push it too far into the realm of "teaching," finding that delicate balance of working within his window of tolerance for demands while also facilitating his learning. It's an ever evolving equilibrium, and who knew it would ever involve algebra with kitties, cows, and fish!

Previous Post - Next Post